This work shows how to learn a thrust-attitude controller for a quadrotor through model-based reinforcement learning by leveraging a learnt probabilistic model of drone dynamics. Little prior knowledge of the flight dynamics is assumed; instead, a sequential latent variable model is learnt from raw sensory input. The controller and value function are optimised entirely in simulation by propagating stochastic analytic gradients through generated latent trajectories. Without any modifications, this controller is then deployed on a self-built drone and is capable of flying the drone to a randomly placed marker in an enclosed environment. Achieving this requires less than 30 minutes of real-world interactions.

The work is published in BeckerEhmck et al. (2020).

Motivation

Reinforcement learning (RL) has only achieved limited impact on real-time robot control due to its high demand of real-world interactions and the complexity of continuous control tasks. However, if successful, RL promises broad applicability as it is a very general approach requiring virtually no prior knowledge of the underlying system. Our main goal with this work is to show that real-world robot control with minimal engineering is becoming feasible with state of the art black-box methods for model estimation and policy optimisation. We show this at the example of a self-built drone, but it is important to understand the method in theory is not specific to the experimental setting discussed here.

Method

At the core our method consists of two parts. First, we learn a probabilistic forward dynamics model of the drone and then we use this model to optimise a controller using an on-policy Actor-Critic reinforcement learning method.

Variational Latent State Space Model

To learn the dynamics, we propose the use of a switching linear dynamical systems which we optimise using neural variational inference methods as proposed in BeckerEhmck et al. (2019). This is a black-box method for learning a generative model of any sequential data that may also be used as an online filter for state estimation. We have found locally linear dynamics to be a very good fit requiring less data for many robotic settings when compared to typical (gated) RNN or feedforward transition models.

At a high level, this method falls into the family of variational state-space models or, more broadly, sequential latent-variable models which we optimise using the vanilla Evidence Lower Bound (ELBO) with only some KL-annealing at the start of training:

Model-Based Actor-Critic

We propose a model-based Actor-Critic variant that relies entirely on simulated rollouts using the previously described model for both policy optimisation and value estimation. Policy (actor) and value function (critic) are both parametrised by neural networks. Given that our model is differentiable, we can use first-order information by backpropagating stochastic analytic gradients through the simulated rollouts allowing for fast optimisation of both actor and critic.

For value estimation, our loss function is the \(n\)-step temporal difference where a Monte Carlo estimation is used for the first \(n\) steps before the approximated value of the terminal state is plugged in:

The horizon \(H\) allows us to limit how far we trust the model to make accurate predictions. We use values up to \(10\), which is considered long in the reinforcement learning world. Similar to the critic's optimisation procedure, the policy is improved by taking the gradient of a short simulated rollout together with the estimated value of the final state of the trajectory:

Using a critic in such a way for policy evaluation is the main characteristic for Actor-Critic methods.

Relying on the model as much as we do has been problematic even on simulated tasks for many previous methods. These problems have been attributed to modelling errors which allow the policy to exploit inaccuracies in the model to learn behaviour inapplicable to the real system. That our method works speaks volumes to the quality of the sequential model that we learn even from noisy real-world data. We do note, however, that learning a critic is vital to success as optimising purely on Monte Carlo rollouts using an episodic model-based policy gradient algorithm does not yield any success.

Our Drone

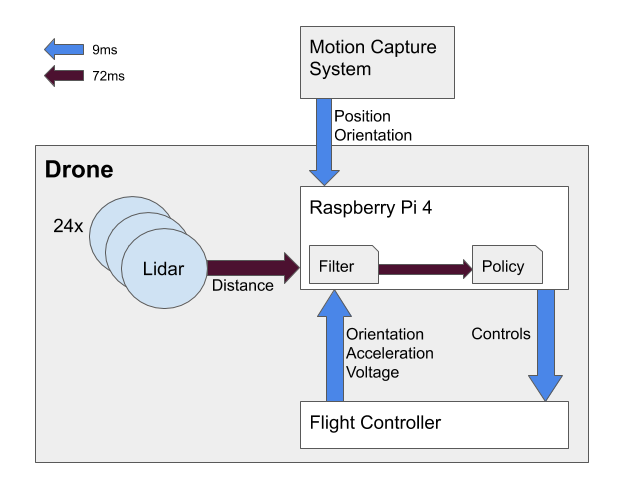
Our self-made drone is purpose-built for machine learning, featuring a sturdy frame allowing for collisions and crashes at moderate speeds while staying fully operational. It is equipped with 24 LiDARs (VL53L1X), motion capture markers, a Raspberry Pi 4 and flight controller with an IMU (ICM-20602). All necessary computations, meaning both the learnt model used as a filter for online state estimation and the policy, are executed onboard.

You can download the source code of mechanical parts of the drone below.

Experimental Results

In our experiments we showcase various scenarios using different subsets of the available sensors. We fly with full state observation (position and velocity) provided by a motion capture system, with only the motion capture positions without observed velocities and without any motion capture at all, relying entirely on the onboard sensors for state estimation and learning of dynamics. The full setting and results are discussed in the following video:

Outlook

This is just a first, but important, step towards bringing (model-based) reinforcement learning to real robot control. A few caveats remain, we would like to directly perform control on motor currents instead of thrust-attitude commands and the engineered initial exploration scheme to learn an initial dynamics model is unsatisfactory. However this work does highlight the potential of an almost fully learnt agent and shows that, with minimal engineering, this robot-agnostic framework is already good enough to perform a simple task on a real, complex system.

Engineered methods will remain better until they are not.

open-source drone hardware arXiv